
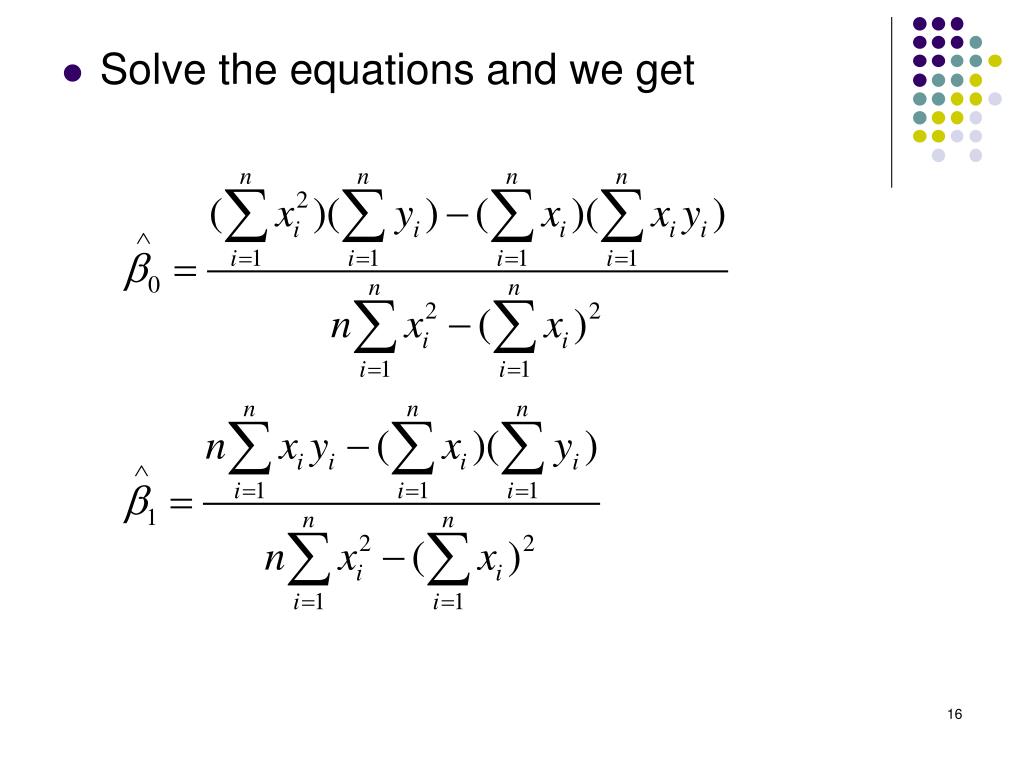
The obvious fix is to make the function \(f(X)\) actually depend on \(x\). Many of the data points are very far from the orange line representing \(c\). (Some function \(f(X) = c\).) In the plot below, we see this doesn’t seem to do a very good job. That is, the model for \(y\) does not depend on the value of \(x\). We could try to model the data with a horizontal line. What sort of function should we use for \(f(X)\) for the cars data? You could think of this a number of ways: This indicates that if we plug in a given value of \(X\) as input, our output is a value of \(Y\), within a certain range of error. The function \(f\) describes the functional relationship between the two variables, and the \(\epsilon\) term is used to account for error. In the cars example, we are interested in using the predictor variable speed to predict and explain the response variable dist.īroadly speaking, we would like to model the relationship between \(X\) and \(Y\) using the form For example, when trying to predict a person’s weight given their height, would it be accurate to say that height is independent of weight? Certainly not, but that is an unintended implication of saying “independent variable.” We prefer to stay away from this nomenclature. While these other terms are not incorrect, independence is already a strictly defined concept in probability. However, those monikers imply mathematical characteristics that might not be true. Other texts may use the term independent variable instead of predictor and dependent variable in place of response. The predictor variable is used to help predict or explain the response (target, outcome) variable, \(y_i\). We use \(x_i\) as the predictor (explanatory) variable. We use \(i\) as an index, simply for notation. We have pairs of data, \((x_i, y_i)\), for \(i = 1, 2, \ldots n\), where \(n\) is the sample size of the dataset. Plot(dist ~ speed, data = cars, xlab = "Speed (in Miles Per Hour)", ylab = "Stopping Distance (in Feet)", main = "Stopping Distance vs Speed", pch = 20, cex = 2, col = "grey")
14.1.1 Variance Stabilizing Transformations.11.3.1 Factors with More Than Two Levels.11 Categorical Predictors and Interactions.9.2.3 Confidence Intervals for Mean Response.8.10 Significance of Regression, F-Test.8.8 Prediction Interval for New Observations.8.7 Confidence Interval for Mean Response.8.6.2 Significance of Regression, t-Test.8.4 Confidence Intervals for Slope and Intercept.8.2.1 Simulating Sampling Distributions.8 Inference for Simple Linear Regression.7.5 Maximum Likelihood Estimation (MLE) Approach.6.4 Quick Comparisons to Other Languages.


 0 kommentar(er)
0 kommentar(er)
